实验二：图像复原

实验目的

  1. 利用反向滤波和维纳滤波进行降质图像复原，比较不同参数选择对复原结果的影响。

实验

实验内容

  1. 利用反向滤波方法进行图像复原；
  2. 利用维纳滤波方法进行图像复原。

实验环境

  • macOS 14.1 Sonoma（Apple M1 PRO）
  • PyCharm/Python3.10
  • OpenCV-Python

实验原理及过程

  1. 输入图像采用实验 1 所获取的图像，对输入图像采用运动降质模型，如下式所示

    H(u,v)=Tπ(au+bv)sin⁡[π(au+bv)]exp⁡−jπ(au+bv)u,v=−N2,−N2+1,...,−1,0,1,...,N2−1T=1,a=b=0.02H(u,v)=\frac{T}{\pi(au+bv)}\sin[\pi(au+bv)]\exp^{-j\pi(au+bv)}\\ u,v=-\frac{N}{2},-\frac{N}{2}+1,...,-1,0,1,...,\frac{N}{2}-1\\ T=1,a=b=0.02

    • 读取灰度图：

      1
      2
      3
      4
      5
      6
      # 读入彩图,转换灰图
      image = cv.imread('../lena512color.png')
      gray_lena = color2gray(image)
      print(gray_lena.shape)
      # (512, 512)
      N = 512

    • 生成PSF的傅立叶变换（降质系统的传递函数HH）

      • 先定义函数，再利用列表推导式生成HH矩阵（数组）
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      def H(u, v):
          """
          psf的fft
          :param u: 
          :param v: 
          :return: 
          """
          a, b = 0.02, 0.02
          T = 1
          tmp = np.pi * (a * u + b * v)
          if tmp == 0:
              return T
          return (T / tmp) * np.sin(tmp) * np.exp(-1j * tmp)

      H_func = np.array(
          [[H(u, v) for v in arange(-N / 2, N / 2)] for u in arange(-N / 2, N / 2)],
          dtype=np.complex128)

    • 运动降质实现如下：

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      def make_blur(src_img, psf):
          """
          运动降质
          :param src_img: 原始图片
          :param psf: psf的fft
          :return: 降质图片
          """
          # fft + shift
          fft_src_img = fftshift(fft2(src_img))
          # 降质
          G = fft_src_img * psf
          # 逆（fft + shift）
          G_ifft = ifft2(ifftshift(G))
          # 转为uint8
          g_img = np.abs(G_ifft)
          return g_img

      gray_lena_blurred = make_blur(gray_lena, H_func)
      imgWrite(gray_lena_blurred, "实验二：图像复原/gray_lena_blurred.png")
      • 降质后图像（gray_lena_blurred）如下：
        gray_lena_blurred

  2. 没有噪声的情况下，对降质后的图像进行反向滤波和维纳滤波操作，得到复原图像

    • 反向滤波(无噪声)：

      • 傅立叶变换估计：

        F^(u,v)=G(u,v)H(u,v)\hat{F}(u,v)=\frac{G(u,v)}{H(u,v)}

        • 猜测由于python的精度问题，1H\frac{1}{H}会有极小值问题（测试H∗1H≠onesnH*\frac{1}{H}\neq ones_n），而是会有1e−161e^{-16}这种小数字，会导致FF变的极大，导致傅立叶变换出现问题。
        • 助教给出的解决方案是建议我使用频域上的G(u,v)G(u,v)直接反向滤波，但这好像并没有什么实际意义
        • 故手动添上一个eps=e−3/e−4eps=e^{-3}/e^{-4}，这会避免上述极小值被除导致的异常。但是并不会达到理论上几乎完美（因为本身也会有abs/real的量化）的反向滤波效果。（后续实验均在此基础上进行）
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        eps = 1e-3
        def inverse(g_src_img, psf):
            """
            无噪反向滤波
            :param g_src_img: 降质图像
            :param psf: psf的fft
            :return: 滤波处理后的图像
            """
            fft_G_img = fftshift(fft2(g_src_img))
            # 精度问题，需添加eps
            F = fft_G_img / (psf + eps)
            F_ifft = ifft2(ifftshift(F))
            f_img = np.abs(F_ifft)
            return f_img

      • 反向滤波实现：

        1
        2
        3
        # 逆滤波
        inv_gray_lena = inverse(gray_lena_blurred, H_func)
        imgWrite(inv_gray_lena, "实验二：图像复原/inv_gray_lena.png")
        • 反向滤波效果图（inv_gray_lena）如下：
          inv_gray_lena

    • 维纳滤波：

      • 傅立叶变换估计：

        F^(u,v)≈[1H(u,v)⋅∣H(u,v)2∣∣H(u,v)∣2+K]G(u,v)\hat{F}(u,v)\approx[\frac{1}{H(u,v)}\cdot\frac{\lvert H(u,v)^2\rvert}{\lvert H(u,v)\rvert^2+K}]G(u,v)

        • 目前测试取K=0.05K=0.05，后续会最优求解

      • 维纳滤波实现：

        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        16
        17
        def wiener(g_src_img, psf, k):
            """
            weiner滤波
            :param g_src_img: 降质图像
            :param psf: psf的fft
            :param k: 常数
            :return: 滤波处理后的图像
            """
            fft_G_img = fftshift(fft2(g_src_img))
            F = (np.abs(psf * psf) / (np.abs(psf) ** 2 + k)) * fft_G_img / psf
            F_ifft = ifft2(ifftshift(F))
            f_img = np.abs(F_ifft)
            return f_img

        # wiener滤波
        wiener_gray_lena = wiener(gray_lena_blurred, H_func, 0.05)
        imgWrite(wiener_gray_lena, "实验二：图像复原/wiener_gray_lena.png")
        • 维纳滤波效果图（wiener_gray_lena）如下：
          wiener_gray_lena

  3. 对降质后的图像施加均值为 0，方差为 10 的高斯噪声，对降质后的图像进行反向滤波和维纳滤波操作，得到复原图像。

    • 添加高斯噪声（使用ex1的函数）

      1
      2
      3
      # 添加高斯噪声
      gray_lena_blurred_gauss = addGaussNoise(gray_lena_blurred, 10)
      imgWrite(gray_lena_blurred_gauss, "实验二：图像复原/gray_lena_blurred_gauss.png")

      • 添加噪声后的降质图像（gray_lena_blurred_gauss）如下：

        gray_lena_blurred_gauss

    • 对降质有噪图像进行反向滤波：

      1
      2
      3
      # 高斯逆滤波
      inv_gray_lena_gauss = inverse(gray_lena_blurred_gauss, H_func)
      imgWrite(inv_gray_lena_gauss, "实验二：图像复原/inv_gray_lena_gauss.png")

      • 效果图（inv_gray_lena_gauss）如下，可见无法复原：

        inv_gray_lena_gauss

    • 对降质有噪图像进行维纳滤波：

      1
      2
      3
      # 高斯wiener滤波
      wiener_gray_lena_gauss = wiener(gray_lena_blurred_gauss, H_func, 0.05)
      imgWrite(wiener_gray_lena_gauss, "实验二：图像复原/wiener_gray_lena_gauss.png")

      • 效果图（wiener_gray_lena_gauss）如下，可以复原，但仍有噪点：

        wiener_gray_lena_gauss

  4. 在加噪声的情况下，对每一种方法通过计算复原出来的图像的峰值信噪比，进行最优参数的选择，包括反向滤波方法中进行复原的区域半径𝑟0𝑟_0（这里r0r_0指恢复频谱边缘到图像中心的像素点距离，实验时统一用像素个数/图像宽高像素数）、维纳方法中的噪声对信号的频谱密度比值𝐾。

    • 最优参数寻找思路：

      • 设定最优参数遍历区间，计算复原图像与原灰度图的PSNR，保留最大值及其对应参数，该参数即为最优参数。（一开始只保留了最大值PSNR，但后续要画图，故将代码改为保留PSNR和参数列表）

    • 反向滤波最优复原半径：

      • 反向滤波（复原半径）实现：本质上是一个低通滤波器
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        def inverse_H(g_src_img, r):
            """
            反向滤波（r）
            :param g_src_img: 降质加噪图像
            :param r: 复原半径
            :return:
            """
            h = np.array(
                [[1 / H(u, v) if u ** 2 + v ** 2 <= r ** 2 else 0 for v in arange(-N / 2, N / 2)] 
                 for u in arange(-N / 2, N / 2)], dtype=np.complex128)
            fft_G_img = fftshift(fft2(g_src_img))
            F = fft_G_img * h
            F_ifft = ifft2(ifftshift(F))
            f_img = np.abs(F_ifft)
            return f_img
      • 最优半径寻找实现：
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        16
        def optimal_inverse(src_img, g_src_img, minr, maxr):
            """
            寻找反向滤波最优复原半径
            :param src_img: 原始灰度图
            :param g_src_img: 降质加噪图
            :param minr: 最小半径
            :param maxr: 最大半径
            :return: 最大psnr及其对应r
            """
            psnr_lst, r_lst = [], arange(minr, maxr, 0.1)
            for r in r_lst:
                i_img = inverse_H(g_src_img, r)
                psnr_lst.append(psnr(src_img, i_img))
            subplot(211)
            plot(r_lst, psnr_lst, ls="-", label="Radius")
            return np.max(psnr_lst), r_lst[np.argmax(psnr_lst)]

    • 维纳滤波最优频谱密度比值K：

      • 最优频谱密度比值寻找实现：
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        16
        def optimal_wiener(src_img, g_src_img, mink, maxk):
            """
             寻找最优频谱密度比值
            :param src_img: 原始灰度图
            :param g_src_img: 降质加噪图
            :param mink: 最小k
            :param maxk: 最大k
            :return: 最大psnr及其对应k
            """
            psnr_lst, k_lst = [], arange(mink, maxk, 0.01)
            for k in k_lst:
                w_img = wiener(g_src_img, H_func, k)
                psnr_lst.append(psnr(src_img, w_img))
            subplot(212)
            plot(k_lst, psnr_lst, ls="-", label="K")
            return np.max(psnr_lst), k_lst[np.argmax(psnr_lst)]

    • 最优值寻找，并画图：

      1
      2
      3
      print(f"inverse-blurred-gauss-PSNR:{optimal_inverse(gray_lena, gray_lena_blurred_gauss, 32, 35)}")
      print(f"wiener-blurred-gauss-PSNR:{optimal_wiener(gray_lena, gray_lena_blurred_gauss, 0.01, 0.1)}")
      savefig("实验二：图像复原/opt-psnr.png", dpi=300)
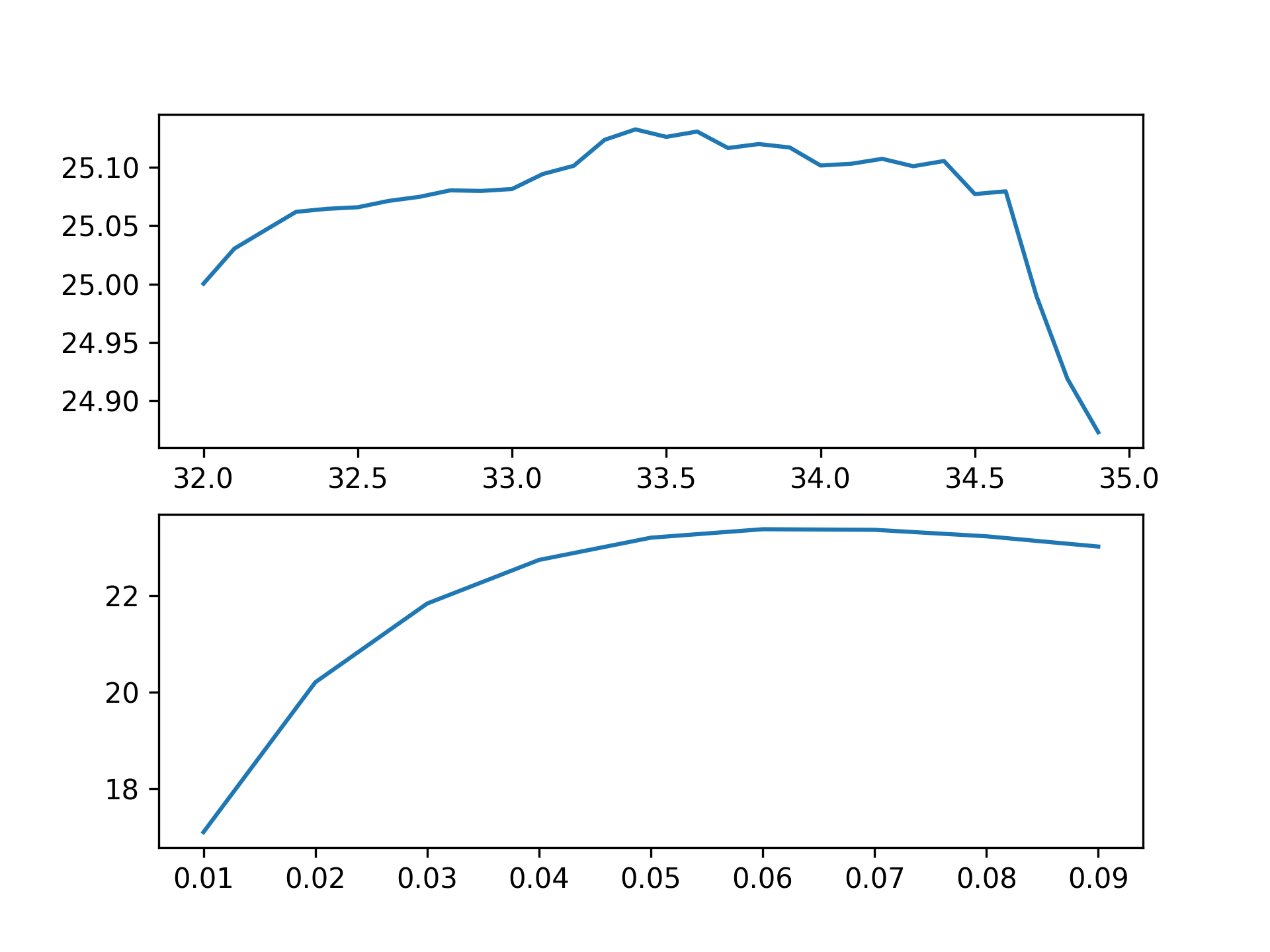
      • 统计图（opt-psnr.png）如下：
        opt-psnr
      • 对于降质有噪图像最优参数为：半径r=33.4,k=0.06r=33.4,k=0.06

  5. 将降质图像和利用最优参数恢复后的图像同时显示出来，以便比较

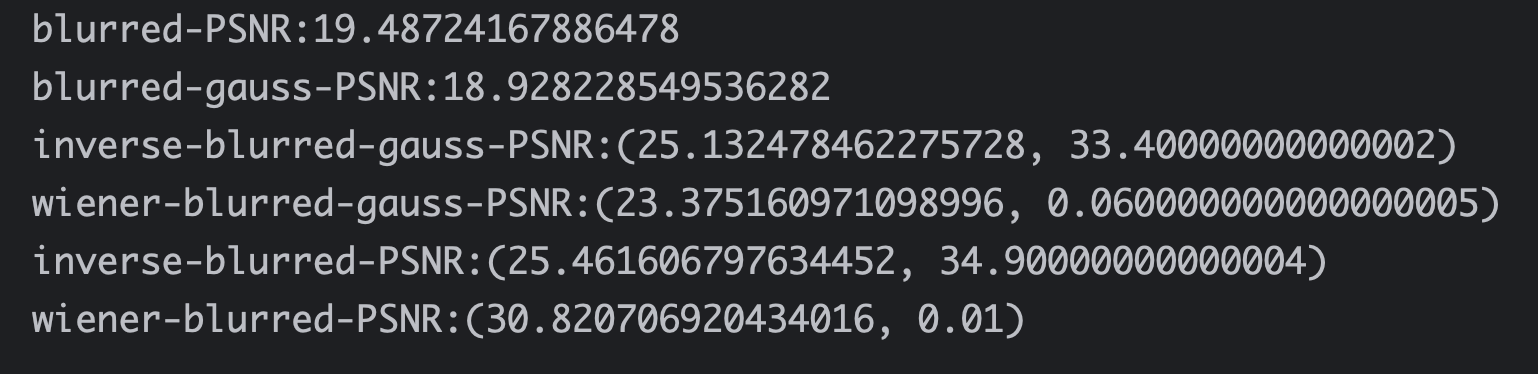
  • 恢复图像（compare）对比如下（顺序与ppt一致）：
    compare
  • 最优参数与PSNR如下：

    image-20231128113731412