imgProc-ex1

实验一：图像去噪

实验目的

1. 熟悉和掌握 Python 图像处理的基本操作；
2. 掌握 DCT 变换的基本性质和 Python 的实现方法；
3. 掌握如何利用 DCT 变换进行简单的图像去噪任务；
4. 掌握如何利用 Python 进行 PSNR 等图像质量评价客观标准。

实验内容

• 对 Lena 图像进行基础的图像处理操作，对图像进行添加噪声、去噪处理的操作
• 计算去噪处理之后图像与添加噪声前图像的 PSNR

实验环境

• macOS 14.1 Sonoma（Apple M1 PRO）
• PyCharm/Python3.10
• OpenCV-Python

实验原理及过程

1. 读取 Lena 图像，将彩色图转换为灰度图

   • 数字图像的表示:

     • 一幅图像可以被定义为一个二维函数$𝑓(𝑥, 𝑦)$，其中$𝑥$和$𝑦$是平面坐标，$𝑓$在每一个坐标处的取值$𝑘\in 𝑅^r$即为图像在该点的亮度和色彩。灰度图像对于每一个坐标$(𝑥, 𝑦)$有$𝑓(𝑥, 𝑦) = 𝑘 \in 𝑅$来代表图像的灰度信息。同样，RGB
       彩色图像可以看作是一幅图像在三原色通道上的不同灰度图像的加和
     • 自然灰度图像关于$𝑥, 𝑦$和幅度连续，但将自然图像转化为数字图像时，需要将坐标和振幅进行数字化处理，通过采样和量化将灰度图像变为一个$𝑚 × 𝑛$矩阵。
     • 如果使用uint8表示则数据取值范围是$[0,255]\in \mathbb{N}$，如果使用float则需要归一化，即数据取值范围是$[0,1]\in \mathbb{R}$

   • python中OpenCV库的安装

     • 前者是标准库，后者是扩展库，二者不可兼容

     pip install opencv-python
     pip install opencv-contrib-python

   • 读取Lena图像

     image = cv.imread('../lena512color.png')

   • 彩色图转换为灰度图

     def color2gray(img):
         """
         将彩色图转为灰度图
         :param img: 彩色图
         :return: 灰度图
         """
         gray_image = cv.cvtColor(img, code=cv.COLOR_BGR2GRAY)
         return gray_image
     
     gray_lena = color2gray(image)

   • 便于实验，图片保存至本地

     def imgWrite(src, dst):
         cv.imwrite(dst, src)
         
     imgWrite(gray_lena, "./images/gray.jpg")

   • 灰度图结果

     

2. 添加均值为 0，标准差$\sigma$分别为 10、20、30、40 的高斯噪声

   • 高斯噪声，也称为白噪声或随机噪声，是一种符合高斯（正态）分布的随机信号或干扰。它的特点是在所有频率上具有恒定的功率谱密度，使其在不同频率上呈现出等能量的随机波动。

     $$G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}$$

   • 添加高斯噪声

     • 需要注意的是不要在任何图像处理的过程中提前量化，由于一开始uint8的使用导致后续PSNR的结果有一定误差,后续在助教和同学的帮助下修改了这一「提前量化」的错误。

     def addGaussNoise(src, sigma):
         """
         添加高斯噪声
         :param src: 原始图像
         :param sigma: 标准差
         :return: 加高斯噪声的图像
         """
         # 平均值
         mean = 0
         # 获取图片的高度和宽度
         height, width = src.shape
         # 生成高斯噪声
         gauss = np.random.normal(mean, sigma, (height, width))
         # gauss = np.random.randn(height, width) * sigma
         # 添加高斯噪声(不要使用uint8提前量化，会损失精度)
         noisy_img = np.float32(src) + gauss
         # 设置图片添加高斯噪声之后的像素值的范围
         noisy_img = np.clip(noisy_img, a_min=0, a_max=255)
         return noisy_img
     
     gaussImages = []
     segmas = [10, 20, 30, 40]
     for s in segmas:
         gaussImages.append(addGaussNoise(gray_lena, s))
         imgWrite(gaussImages[s // 10 - 1], f"./images/gauss{s}.png")

   • 添加高斯噪声的结果 :

     

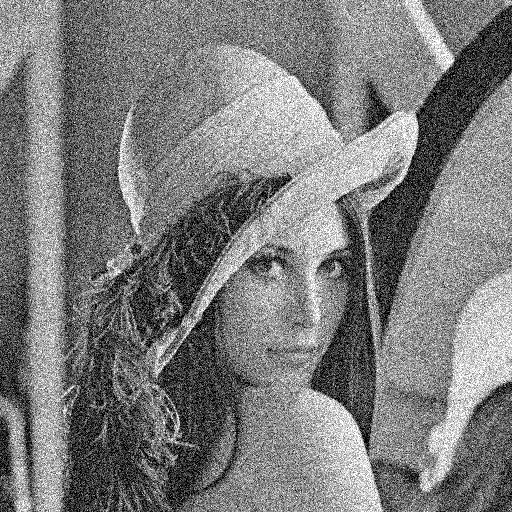
3. 计算不同噪声下的图像的 PSNR 值

   • PSNR

     • 全称Peak Signal-to-Noise Ratio，即峰值信噪比，是衡量图像质量的指标之一。

     • 对给定一个大小为$m*n$的原始图像$I$和对其添加噪声后的噪声图像$K$，PSNR是基于MSE(均方误差)定义

   • MSE可定义为：

     $$MSE=\frac{1}{mn}\sum_{i=0}^{m-1}\sum_{i=j}^{n-1}[I(i,j)-K(i,j)]^2$$

   • PSNR可定义为：

     $$PSNR=10log_{10}(\frac{MAX_I^2}{MSE})=20log_{10}(\frac{MAX_I}{\sqrt{MSE}})$$

   • python实现

     • 手写实现

     # https://blog.csdn.net/u010886794/article/details/84784453
     def psnr(img1, img2):
         """
         计算PSNR（归一）
         :param img1: 基准图像
         :param img2: 测试图像
         :return:
         """
         mse = np.mean((img1 / 255. - img2 / 255.) ** 2)
         PIXEL_MAX = 1
         return 20 * math.log10(PIXEL_MAX / math.sqrt(mse))
     
     PSNR = list(map(psnr, [gray_lena] * 4, gaussImages))
     print(f"PSNRs is {PSNR}")

     • 第三方库：

       pip install scikit-image

       from skimage.metrics import peak_signal_noise_ratio as psnr

     • 计算结果

       | $\sigma$ | 10 | 20 | 30 | 40 |
       | :------: | :–: | :–: | :–: | :–: |
       | PSNR | 28 | 22 | 18 | 16 |

       

4. 图像去噪：对噪声图像进行 DCT 变换（8x8 图像块尺寸），按照$3\sigma$阈值对变换域上的系数进行处理,对处理后的系数进行 DCT 反变换，得到去噪后的图像

   • DCT变换（离散余弦变换）

     $$C(u,v)=\frac{2}{N}\sum_{x=0}^{N-1}\sum_{y=0}^{N-1}f(x,y)[cos\frac{(2x+1)u\pi}{2N}][cos\frac{(2y+1)v\pi}{2N}]$$

   • python实现

     def denoise_DCT(img, sigma, psize=8):
         """
         DCT去噪
         :param img: 原始图片
         :param sigma: 标准差
         :param psize: DCT处理尺寸
         :return:
         """
         # 将图像分成8x8的块
         height, width = img.shape
         new_height = np.int32(np.ceil(height / psize) * psize)
         new_width = np.int32(np.ceil(width / psize) * psize)
         padded = np.zeros((new_height, new_width))
         padded[:height, :width] = img
         blocks = [np.float32(padded[i:i + psize, j:j + psize]) for i in range(0, new_height, psize) for j in range(0, new_width, psize)]
         # 对每个块进行DCT变换
         for block in blocks:
             block -= 128  # 将像素值平移到均值为0
             dct = cv.dct(block)
             # 对DCT系数进行3sigma阈值处理
             mask = np.abs(dct) > 3 * sigma
             dct = dct * mask
             # 对处理后的DCT系数进行逆DCT变换
             block[:] = cv.idct(dct) + 128  # 逆变换并平移回原始范围
         # 重新构建图像
         denoised_image = np.zeros((new_height, new_width))
         for i, block in enumerate(blocks):
             y = (i // (new_width // psize)) * psize
             x = (i % (new_width // psize)) * psize
             denoised_image[y:y + psize, x:x + psize] = block
         # 裁剪回原始图像尺寸
         denoised_image = denoised_image[:height, :width]
         denoised_image = np.uint8(denoised_image)
         return denoised_image
     
     gaussImages_DCT = []
     for s in segmas:
         gaussImages_DCT.append(denoise_DCT(gaussImages[s // 10 - 1], s, 8))
         imgWrite(gaussImages_DCT[s // 10 - 1], f"./images/gauss{s}_DCT.png")

   • DCT去噪结果:

     

5. 计算去噪之后的图像的 PSNR 值

   • python实现

     PSNR_DCT = list(map(psnr, [gray_lena] * 4, gaussImages_DCT))
     print(f"PSNR_DCTs is {PSNR_DCT}")

   • 计算结果

     | $\sigma$ | 10 | 20 | 30 | 40 |
     | :------: | :–: | :–: | :–: | :–: |
     | PSNR | 28 | 22 | 18 | 16 |
     | PSNR_DCT | 32 | 28 | 26 | 24 |

     

思考题

1. 在分块 DCT 的条件下还有什么方式可以进行图像去噪？

   • 不太明白在DCT变换域条件下，除了滤掉高频部分还有什么办法。。。

2. 实验中的去噪方法会对原图像造成什么影响

   • 由于分块处理，会导致结果分块边缘明显，不够平滑